Razão
Conceitualmente a razão do número a para o número b, sendo b ≠ 0, é igual ao
quociente de a por b que podemos representar das
seguintes formas:
As razões acima podem ser lidas como:
- razão de a para b
- a está para b
- a para b
Em qualquer razão, ao termo a chamamos de antecedente
e ao termo b chamamos de consequente.
Razão inversa ou recíproca
Vejamos as seguintes razões:
Elas são tidas como razões inversas ou recíprocas.
Note que o antecedente de uma é o consequente da
outra e vice-versa.
Uma propriedade das razões inversas é que o produto
delas é sempre igual a 1. Isto se deve ao fato de uma ser o inverso
multiplicativo da outra.
Agora vejamos as seguintes razões:
A primeira razão possui os números 1 e 2 como seu
respectivo antecedente e consequente, já a segunda razão possui o número 2 como
o seu antecedente e o número 1, omitido, como o seu consequente. Em função
disto, pelo antecedente de uma ser o consequente da outra e vice-versa, estas
duas razões também são inversas uma em relação a outra.
Apesar de uma razão ser apresentada na forma de uma
fração ou de uma divisão, você pode calcular o seu valor final a fim de se
obter o seu valor na forma decimal. Por exemplo:
A razão de 15
para 5 é 3, pois 15 : 5 = 3
na forma decimal, ou seja, 15 é
o triplo de 5.
Neste outro caso, a razão de 3 para 4 é 0, 75, pois 3: 4 = 0,75 na forma decimal.
Razão centesimal
Como visto acima, a razão de 3 para 4 é 0, 75, pois 3: 4 = 0,75 na forma decimal, ou seja,
3 equivale a 75% de 4. 75% nada mais é
que uma razão de antecedente igual 75
e consequente igual a 100. É por
isto é chamada de razão centesimal.
Exemplos
O salário de Paulo é de
R$ 2.000,00 e João tem um salário de R$ 1.000,00. Qual a razão de um salário
para outro?
Temos: Salário
de Paulo: Salário de João.
Então:
A razão acima pode ser lida como a razão de 2000
para 1000, ou 2000 está para 1000. Esta razão é igual a 2, o que equivale a
dizer que o salário de Paulo é o dobro do salário de João, ou seja, através da
razão estamos fazendo uma comparação de grandezas, que neste caso são os
salários de Paulo e João.
Portanto a razão de um
salário para outro é igual a 2.
Eu tenho uma estatura de
1,80m e meu filho tem apenas 80cm de altura. Qual é a razão de nossas alturas?
Como uma das medidas está em metros e a outra em
centímetros, devemos colocá-las na mesma unidade. Sabemos que 1,80m é
equivalente a 180 cm.
Temos então a razão de 180 cm
para 80 cm:
2,25 é a razão de nossas
alturas.
Proporção
A igualdade entre razões denomina-se proporção.
Os números a,
b, c e d, todos
diferentes de zero, formam nesta ordem, uma proporção se, e somente se, a razão
a: b for igual à razão c: d.
Indicamos esta proporção por:
Chamamos aos termos a e d de extremos e aos termos b e c chamamos de meios.
Veja que a razão de 10 para 5 é igual a
2 (10: 5 = 2).
A razão de 14
para 7 também é igual a 2 (14: 7 = 2).
Podemos então afirmar que estas razões são iguais e
que a igualdade abaixo representa uma proporção:
Lê-se a proporção acima da seguinte forma:
"10 está para 5, assim
como 14 está para 7".
Propriedade fundamental das proporções
Qualquer que seja a proporção, o produto dos
extremos é igual ao produto dos meios. Assim sendo, dados os números a, b, c e d, todos diferentes de zero e formando
nesta ordem uma proporção, então o produto de a por d será igual
ao produto de b por c:
Segunda propriedade das proporções
Qualquer que seja a proporção, a soma ou a
diferença dos dois primeiros termos está para o primeiro, ou para o segundo
termo, assim como a soma ou a diferença dos dois últimos termos está para o
terceiro, ou para o quarto termo. Então temos:
Ou
Terceira propriedade das proporções
Qualquer que seja a proporção, a soma ou a
diferença dos antecedentes está para a soma ou a diferença dos consequentes,
assim como cada antecedente está para o seu respectivo consequente. Temos
então:
Ou
Quarta proporcional
Dados três números a, b, e c, chamamos de quarta proporcional o
quarto número x que junto a eles
formam a proporção:
Tendo o valor dos números a, b, e c, podemos obter o valor da quarta
proporcional, o número x,
recorrendo à propriedade fundamental das proporções. O mesmo procedimento
utilizado na resolução de problemas de regra de três simples.
Terceira proporcional
Em uma proporção onde os meios são iguais, um dos
extremos é a terceira proporcional do outro extremo:
Na proporção acima a é a terceira proporcional de c e vice-versa.
Exemplos
Paguei R$15,00 por 1kg de
carne. Se eu tivesse pago R$25,00 teria comprado 2kg. A igualdade da razão do
preço de compra pela quantidade, dos dois casos, resulta em uma proporção?
Os termos da nossa suposta proporção são: 15, 1, 25 e 2.
Podemos utilizar a propriedade fundamental das
proporções para verificamos se tais termos nesta ordem formam ou não uma
proporção.
Temos então:
Como 30 difere de 25, não temos uma igualdade,
consequentemente não temos uma proporção.
Poderíamos também ter analisado as duas razões:
Como as duas razões possuem valores diferentes,
obviamente não se trata de uma proporção.
Como uma das razões
resulta em 15 e a outra resulta em 12,5, concluímos que não se trata de uma
proporção, já que 15 difere de 12,5.
A proporção não ocorreu porque ao comprar 2kg de
carne, eu obteria um desconto de R$ 2,50 no preço do quilograma, o que deixaria
as razões desproporcionais.
A soma de dois números é
igual a 240. Sabe-se que um deles está para 5, assim como o outro está para 7.
Quais são estes números?
Para a resolução deste exemplo utilizaremos a
terceira propriedade das proporções. Chamando um dos números de a e o outro de b, podemos montar a seguinte proporção:
Sabemos que a soma de a com b resulta em 240, assim como a adição de 5 a
7 resulta em 12. Substituindo estes valores na
proporção teremos:
Portanto:
Concluímos então que os
dois números são 100 e 140.
Quatro números, todos
diferentes de zero, 10, 8, 25 e x formam nesta ordem uma proporção. Qual o
valor de x?
Seguindo o explicado sobre a quarta proporcional
temos:
O valor do número x é 20.
Exercícios
1) Dois números somados totalizam 510. Sabe-se que um
deles está para 8, assim como o outro está para 9. Quais são os dois números?
Chamemos o primeiro número de a e o outro número de b. Do enunciado, tiramos que a está para 8, assim como b está para 9. Utilizando-nos da
terceira propriedade das proporções temos:
Sabemos que a
e b somados resultam em 510, assim como a adição de 8 a
9 resulta em 17.
Substituindo estes valores na
proporção teremos:
Portanto: Chegamos
então que os dois números são 240 e 270.
2) Um número a somado a um outro número b totaliza 216. a
está para 12, assim como b está para 15. Qual o valor de a e de b?
Recorrendo à terceira propriedade das proporções montamos a seguinte
proporção:
Sabemos que a soma de a
com b é igual a 216, assim como também sabemos que 12 mais 15 totaliza 27.
Substituindo tais valores teremos:
Portanto: Os dois números são 96
e 120.
3) Um número a subtraído de um outro número b resulta em
54. a está para 13, assim como b está para 7. Qual o valor de a e de b?
Recorremos à terceira propriedade das proporções
para montarmos a seguinte proporção:
Sabemos que a diferença entre a e b é igual a 54, e
sabemos também que 13 menos 7 dá 6. Substituindo tais valores teremos:
Portanto: Os
dois números são 117 e 63.
4) A diferença entre dois números é igual a 52. O maior
deles está para 23, assim como o menor está para 19. Quais são os números?
Vamos chamar o número maior de a e o menor de b. Do enunciado, a
está para 23, assim como b está
para 19. Ao utilizarmos a terceira propriedade das proporções temos:
sabemos que a
menos b é igual a 52, assim como 23 menos 19 é igual
a 4. Ao substituirmos estes
valores na proporção teremos:

Portanto:
Chegamos então que os dois números são
299 e 247.
5) A idade de Pedro está para a idade de Paulo, assim como
5 está para 6. Quantos anos tem Pedro e Paulo sabendo-se que as duas idades
somadas totalizam 55 anos?
Identifiquemos a idade de Pedro por a e a idade de Paulo por b. A partir do enunciado, temos que a está para b, assim como 5
está para 6. Utilizando-nos da
segunda propriedade das proporções temos:
Sabemos que a soma a e b resulta em 55, assim como 5 mais 6 resulta em
11. Substituindo estes valores
na proporção temos:
Para calcularmos o valor de a temos:
Portanto: Pedro
tem 25 anos e Paulo tem 30 anos.
6) Dois números a e b diferem entre si em 18 unidades. a
está para b, assim como 825 está para 627. Qual o valor de a e de b?
Da segunda propriedade das proporções temos:
Sabemos que a diferença entre a e b resulta em 18,
assim como 825 menos 627 resulta em 198. Substituindo tais valores na proporção temos:
Para calcularmos o valor de a temos:
Portanto: 75
e 57 respectivamente se referem ao valor de a e de b.





























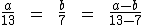


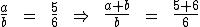




Elizeu França, boa noite!
ResponderExcluirObrigado por acessar o meu blog e por ter gostado do mesmo. Também gostei muito do seu trabalho, com um conteúdo enriquecedor, além de ser muito organizado. Que o blog possa compartilhar inúmeras informações, ideias e experiências no decorrer do seu curso. Já sou um leitor assíduo do seu blog. Irei visitá-lo sempre! Sucesso! Parabéns!
OK,
ResponderExcluirMAS VC FALANDO QUE SERÁ UM LEITOR ASSÍDUO, ME IMPULSIONARÁ A CADA VEZ MAIS POSTAR CONTEÚDOS CADA VEZ MAIS RICOS, VISTO QUE SUA ANÁLISE TERÁ UM GRANDE PESO.
AGRADEÇO A VISITA E CONTINUE SENDO ESSE "SERVO DE DEUS" ILUMINADO E DESEJO MUITO SUCESSO
E SE UM DIA QUISER CONHECER O PANTANAL MATOGROSSENSE, FICA AQUI FEITO O CONVITE, OK?
FELICIDADES MEU AMIGO E DEUS TE ABENÇOE!!!
EIZEU FRANÇA