Medidas de
Comprimento
Unidade
de Comprimento:
|
||||||||||||||||||||||||||||||||||
.
|
||||||||||||||||||||||||||||||||||
A
unidade padrão de comprimento é o metro, esta unidade é conhecida e aceita
por todas as pessoas.
Para medir grandes extensões usamos como unidade
de comprimento um dos múltiplos do metro:
Decâmetro
(dam) Hectômetro (hm) Quilômetro (km)
Para medir pequenas extensões utilizamos como
unidade um dos submúltiplos do metro:
Decímetro
(dm) Centímetro (cm) Milímetro (mm)
Veja
abaixo as unidades de comprimento, seus símbolos e os valores correspondentes
na unidade metro:
|
||||||||||||||||||||||||||||||||||
.
|
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
Exemplos
a) Transformar 5,473 km em metros:
5,473 Km = ( 5,473 x 1000) m = 5473 m
b) Transformar 0,082 hm em metros:
0,082 hm = (0,082 x 100 ) m = 8,2 m
c) transformar 70 cm em metros:
70 cm = ( 70 : 100 ) m = 0,70 m
d) Transformar 92,8 dm em metro:
92,8 dm = ( 92,8 : 10 ) m = 9,28 m
EXERCÍCIOS
1) Transforme em metros:
a) 7 Km (R: 7000 m)
b) 3,4 km (R: 3400 m)
c) 8,16 km (R: 8160 m)
d) 4 dam (R: 40 m)
e) 6,8 hm (R:680m)
f) 0,3 km (R: 300 m)
g) 39 dm (R: 3,9 m)
h) 98,7 dm (R: 9,87 m)
i) 746,3 cm (R: 7,463 m)
j) 59,4 cm (R: 0,594 m)
l) 43,8 dm (R: 4,38 m)
m) 380 mm (R: 0,380m)
2) Faça a conversão de:
a) 7,3 km em m (R: 7300 m)
b) 8,9 m em cm (R:890 cm)
c) 74 dm em cm (R: 740 cm)
d) 2,3 cm em mm (R: 23 mm)
e) 681 cm em dm (R: 68,1 dm)
f) 4786 m em km (R: 4,786 km)
g) 836 cm em dm (R: 83,6 dm)
h) 2,73 dm em cm (R: 27,3 cm)
i) 154 cm em m (R: 1,54 m)
j) 0,94 m em cm (R: 94 cm)
l) 0,81 cm em dm (R: 0,081 dm)
m) 3,97 cm em m (R: 0,0397 m)
a) Transformar 5,473 km em metros:
5,473 Km = ( 5,473 x 1000) m = 5473 m
b) Transformar 0,082 hm em metros:
0,082 hm = (0,082 x 100 ) m = 8,2 m
c) transformar 70 cm em metros:
70 cm = ( 70 : 100 ) m = 0,70 m
d) Transformar 92,8 dm em metro:
92,8 dm = ( 92,8 : 10 ) m = 9,28 m
EXERCÍCIOS
1) Transforme em metros:
a) 7 Km (R: 7000 m)
b) 3,4 km (R: 3400 m)
c) 8,16 km (R: 8160 m)
d) 4 dam (R: 40 m)
e) 6,8 hm (R:680m)
f) 0,3 km (R: 300 m)
g) 39 dm (R: 3,9 m)
h) 98,7 dm (R: 9,87 m)
i) 746,3 cm (R: 7,463 m)
j) 59,4 cm (R: 0,594 m)
l) 43,8 dm (R: 4,38 m)
m) 380 mm (R: 0,380m)
2) Faça a conversão de:
a) 7,3 km em m (R: 7300 m)
b) 8,9 m em cm (R:890 cm)
c) 74 dm em cm (R: 740 cm)
d) 2,3 cm em mm (R: 23 mm)
e) 681 cm em dm (R: 68,1 dm)
f) 4786 m em km (R: 4,786 km)
g) 836 cm em dm (R: 83,6 dm)
h) 2,73 dm em cm (R: 27,3 cm)
i) 154 cm em m (R: 1,54 m)
j) 0,94 m em cm (R: 94 cm)
l) 0,81 cm em dm (R: 0,081 dm)
m) 3,97 cm em m (R: 0,0397 m)
Medidas de Superfícies
Assim como medimos comprimento,
também medimos superfícies planas. Quando falamos em medir uma superfície
plana, temos que compará-la com outra tomada como unidade padrão e verificamos
quantas vezes essa unidade de medida cabe na superfície que se quer medir.
Unidade de Medida de Superfície
Devemos saber que a unidade
fundamental usada para medir superfície é o metro quadrado (m2), que corresponde a área de um quadrado que
possui os lados medindo 1 m cada um.
 |
Este
quadrado possui 1 m de cada lado logo possui um metro quadrado.
|
Quadro de Unidades Usadas para
Medir Superfícies
Múltiplos
|
||
km 2
|
hm 2
|
dam 2
|
1.000.000m
2
|
10.000m
2
|
100m 2
|
Unidade fundamental
|
Submúltiplos
|
||
m2
|
dm 2
|
cm 2
|
mm 2
|
1m 2
|
0,01m 2
|
0,0001m
2
|
0,000001m
2
|
Observe que cada unidade é 100
vezes maior que a unidade imediatamente anterior.
Calculando
Áreas
Área de
Paralelogramos
Lembre-se que paralelogramos são
os quadriláteros que possui os lados opostos paralelos.
Área do Paralelogramo:
 |
Área do
Paralelogramo = Base x Altura
ou
A = b x h |
Área do Quadrado:
 |
Área do Quadrado = Lado x Lado
ou
 |
Área do Retângulo:
 |
Área do
Retângulo = Base x Altura
|
ou
A = b
x h
Área do Losango
 |
 |
Área de
Trapézios
Lembre-se, trapézio não é um
paralelogramo. O trapézio possui apenas dois lados paralelos a base maior e a
base menor.
Área de triângulos
Lembre-se,
triângulo não é paralelogramo e nem trapézio.
Área de um triângulo:
Área do triângulo equilátero:
Triângulo que possui os três lados iguais.
Triângulo que possui os três lados iguais.
A= PI (R) 2, onde R é raio e PI = 3,1416
Exemplos
1. Vamos calcular a área de
um terreno quadrado de 25 m de lado
2. Vamos calcular a área de um campo de futebol
cujas dimensões são 150m de comprimento por 75m de largura. (o campo tem a
forma retangular, com esta na horizontal eu faço comprimento vezes largura) 
Resolva os exercícios abaixo.
1.
Determine a área de um paralelogramo em que a altura mede 10 cm e sua base mede
6 cm. (R = 60)
2.
Sabendo-se que a altura de um triângulo mede 8 cm e sua base
mede 13 cm. Determine sua área. (R = 52)
3. Um losango possui a diagonal maior medindo 8 cm e a menor medindo 6 cm. Calcule a área deste losango. (R = 24)
mede 13 cm. Determine sua área. (R = 52)
3. Um losango possui a diagonal maior medindo 8 cm e a menor medindo 6 cm. Calcule a área deste losango. (R = 24)
4. A
base maior de um trapézio mede 40 cm e sua base menor mede 25 cm. Calcule sua
área sabendo que a altura mede 20 cm. (R = 650)
Observação:
Existem
medidas especificas para medir grandes extensões, como sítios, chácaras e
fazendas.
São
elas o hectare e o are.
1
hectare(ha) = 10.000(m2) 1 are(a) = 100(m2)
Exemplos:
Uma
fazenda possui 120 000 m2 de área, qual a sua medida em hectare?
120.0000
: 10.000 = 120 ha.
Uma
fazenda possui 23,4 ha de área, qual a sua área em m2?
23,4 x
10.000 = 234.000 m2
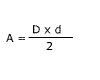
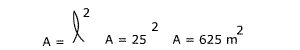
Nenhum comentário:
Postar um comentário
Comente aqui: