13/09/12 - Exercícios de Física

Energia Potencial Gravitacional

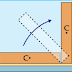
Um pilar de concreto de massa 1,0 t, deitado sobre o solo horizontal, é posto verticalmente de pé (como mostra a figura) usando-se um guindaste. Considere o centro de massa do pilar coincidente com o seu centro geométrico (C).

Nessa operação, adotando g = 10 m/s2, quanto de energia potencial gravitacional foi adicionada ao pilar?

Resolução

O acréscimo ocorrido na energia potencial do pilar de 1000 kg foi promovido pela variação de altura (elevação) do centro de massa do pilar. Isto é, o seu centro (C) eleva-se de h1 = 0,20 m (quando deitado) para h2 = 1,40 m (quando de pé).

Dessa forma, temos:

Epg = m · g · H                 -    H = (1,40 – 0,20) = 1,20

Epg = 1.000 · 10 · 1,20
Epg = 12.000 Joules = 12Kj 

Energia potencial gravitacional 

Da interação gravitacional entre a Terra e um corpo surge a energia potencial gravitacional. Uma energia potencial ou energia armazenada por um corpo é caracterizada pela capacidade deste corpo de realizar  trabalho

No caso da energia potencial gravitacional podemos dar como exemplo uma bola de futebol de 300g (0,3kg) largada a uma altura de 4 metros, observe a figura abaixo.

Todo corpo em queda livre está sujeito a mesma aceleração de direção horizontal e sentido para baixo. Esta aceleração é a aceleração gravitacional (g) que é aproximadamente 9,8 m/s². A força resultante neste movimento é a força peso (P=m.g) e o trabalho desta força é igual a energia potencial gravitacional. Logo, quando a bola é largada a força peso realiza trabalho e a energia potencial gravitacional se transforma em energia cinética.

Para encontrarmos uma equação para a energia potencial gravitacional vamos utilizar a equação do trabalho:

E_p = m.g.h

Sendo assim, para calcularmos a energia potencial gravitacional no nosso exemplo basta substituirmos os valores para a massa do corpo (m), a aceleração gravitacional (g) e a altura em que o corpo se encontra (h).

E_p = m.g.h

E_p =0,3 . 9,8 . 4

E_p = 11,76 J

Energia Potencial Elástica

Exercício 1

Uma mola é deslocada 10cm da sua posição de equilíbrio; sendo a constante elástica desta mola equivalente à 50N/m, determine a energia potencial elástica associada a esta mola em razão desta deformação.

Resposta

x = 10cm = 0,1m

k = 50N/m

E_pel = kx²/2

E_pel = 50.0,1²/2

E_pel = 0,25J

Exercício 2

Um bloco de massa igual a 1kg encontra-se preso sobre uma mola vertical que está deformada 10cm com relação à sua posição de equilíbrio. Após o bloco ser solto, ele é arremessado verticalmente para cima. Sendo o sistema livre de forças dissipativas e a constante elástica da mola equivalente à 50N/m, determine a altura máxima que o bloco alcançará em cm. (obs.: considere a massa da mola desprezível).

Resposta
Quando o bloco atingir a altura máxima, toda energia potencial elástica terá sido convertida em energia potencial gravitacional.

E_pel = E_pg

K.x²/2 = m.g.h

50.0,1²/2 = 1.10.h
0,25 = 10.h
h = 0,25/10
h = 0,025m

--> -->

  Dicas do que é Necessário Para que Você Aprenda

1) Capacidade Sensorio-Motora e Capacidade de Operar Mentalmente

2) Conhecimento Prévio

3) Acesso à Informação

4) Querer

5) Atenção

6) Agir

7) Espressar-se