EQUAÇÃO DO
1º GRAU
EQUAÇÃO ---> IGUALDADE
As equações do primeiro grau são aquelas que
podem ser representadas sob a forma ax+b=0,em que a e b são constantes reais,
com a diferente de 0, e x é a variável. A resolução desse tipo de equação é
fundamentada nas propriedades da igualdade descritas a seguir.
Adicionando um mesmo número a ambos os
membros de uma equação, ou subtraindo um mesmo número de ambos os membros, a
igualdade se mantém.
Dividindo ou multiplicando ambos os membros
de uma equação por um mesmo número não-nulo, a igualdade se mantém.
Exemplo:
Vejamos alguns exemplos:
Seja a equação:
Seja a equação:
Membros de uma equação
Numa equação a expressão situada à esquerda
da igualdade é chamada de 1º membro da equação, e a expressão situada à direita
da igualdade, de 2º membro da equação.
Exemplo: - 3x + 12 = 2x - 9
1º membro 2º membro
Cada uma das parcelas que compõem um membro
de uma equação é chamada termo da equação.
termos
Variável (ou incógnita) de uma equação:
Os elementos desconhecidos de uma equação
são chamados de variáveis ou incógnitas.
Exemplos:
A equação x + 5 = 18 tem uma incógnita: x
A equação x – 3 = y + 2 tem duas incógnitas:
x e y
A equação a² – 3b + c = 0 tem três
incógnitas: a, b e c
Cada um dos valores que, colocados no lugar
da incógnita, transformam a equação em uma sentença verdadeira é chamado de
raiz da equação. Para verificarmos se um dado número é ou não raiz de uma
equação, basta substituirmos a incógnita por esse número e observarmos se a
sentença obtida é ou não verdadeira.
1º exemplo: verificar se três é raiz de 5x –
3 = 2x + 6
2º exemplo: verificar se -2 é raiz de x² –
3x = x – 6
O princípio aditivo e o princípio
multiplicativo servem para facilitar o entendimento da solução de uma equação,
mas para resolvê-la existe um método simples e prático que é o seguinte:
Resolver a equação 5x – 8 = 12 + x
Colocamos no primeiro membro os termos que
apresentam variáveis, e no segundo membro os termos que não apresentam
variável. Os termos que mudam de membro têm os sinais trocados.
5x – 8 = 12 + x
5x – x = 12 + 8
Calculamos a somas algébricas de cada termo.
4.x = 20
Quando se passa de um membro para o outro
usa-se a operação inversa, ou seja, o que está multiplicando passa dividindo
e o que está dividindo passa multiplicando. O que está adicionando passa
subtraindo e o que está subtraindo passa adicionando. O número 4 no primeiro
membro está multiplicando o x então ele passará dividindo no segundo membro.
Exercícios resolvidos:
1) Resolver a equação:
2( x + 5 ) - 3( 5 – x ) = 5
Nesse tipo de equação, devemos inicialmente,
retirar os parênteses, aplicando a propriedade distributiva da multiplicação
e a regra de eliminação de parênteses.
|
3) Resolução da equação:
Nessa equação, inicialmente reduzimos todas
as frações ao mesmo denominador, e a seguir cancelamos esses denominadores.
m.m.c ( 3, 2, 6 ) = 6
3, 2, 6 2
3, 1, 3 3
1, 1, 1 2 . 3 = 6
4) Resolver a equação:
m.m.c ( 2,
3, 4 ) = 12
Efetuando
as multiplicações:
Multiplicando
os dois membros da equação pelo m.m.c dos denominadores, que é 12, vem:
Resolvendo a mesma equação pelo método da
eliminação dos denominadores:
m.m.c ( 2, 3, 4, 5, 7 ) = 420
7) Quando o número x na equação ( k – 3 ).x + ( 2k – 5 ).4 + 4k = 0
vale 3, qual será o valor de K?
( k – 3 ).3 + ( 2k – 5 ).4 + 4k = 0
3k
– 9 + 8k – 20 + 4k = 0
3k
+ 8k + 4k = 9 + 20
15k
= 29
Às vezes, uma equação não tem solução para
um certo universo de números. Nesse caso, dizemos que ela é impossível ou que
a solução é vazia.
Exemplo: resolver a equação.
Não existe nenhum número que multiplicado
por 0 que resulte em 2.
Equação com infinitas soluções
Há casos em que todos os números do universo
considerado são raízes da equação. Dizemos que ela tem infinitas soluções.
Exemplo: resolver a equação
Como qualquer número multiplicado por zero é
igual a zero, a equação tem infinitas soluções.
|
quarta-feira, 22 de agosto de 2012
22/08/12 - Matemática (Eq 1º Grau)
Assinar:
Postar comentários (Atom)
Postagens
-
Muitas pessoas têm dúvidas quanto a diferença entre porcentagem e percentagem . O fato é que tanto porcentagem quanto percenta...
-
1. (CMB/2003 - 6 Ano do E.F.) Numa eleição, 65000 pessoas votaram. O candidato que venceu recebeu 55% do total dos votos. O outro candidat...
-
Medidas de Volumes TABELA DE CONVERSÃO DE UNIDADES: VOLUME m³ cm³ l ft³ in³ 1 met...
-
Energia Potencial Gravitacional Um pilar de concreto de massa 1,0 t, deitado sobre o solo horizontal, é posto verticalmente de pé (...













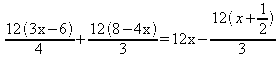










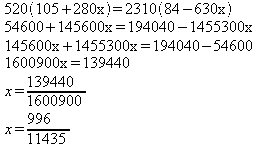
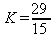





Nenhum comentário:
Postar um comentário
Comente aqui: