_________________________________

Conceitos preliminares

O número p

Dada uma circunferência de raio r, diâmetro d = 2r, o número p é definido como a razão do comprimento C da circunferência pelo seu diâmetro d, isto é,

O comprimento de uma circunferência

Pela definição do número p na equação acima observamos que o comprimento da circunferência é dado por,

Medida de ângulos

Existem 3 unidades para a medida de ângulos

Grado: 1 grado é um ângulo correspondente a 1/400 de uma volta completa da circunferência. Consequentemente, a volta completa na circunferência compreende um ângulo de 400 grados - Figura 1.1(a).

Grau: 1 grau, denotado 1o, é um ângulo correspondente a 1/360 de uma volta completa da circunferência. Consequentemente, a volta completa na circunferência compreende um ângulo de 360o - Figura 1.1(b).

Radiano: 1 radiano, denotado 1 rad, é um ângulo correspondente a um arco de mesmo comprimento do raio da circunferência - Figura 1.1(c).

Conversão grau-radiano

De modo análogo, um arco de comprimento r compreende um ângulo de 1 radiano. A circunferência completa, um arco de comprimento 2 p r, compreende um ângulo q dado por

Exemplo 1.1 Determine a medida do ângulo 3/4p rad em graus.

Exemplo 1.2 Determine a medida do ângulo 155o em radianos

Triângulo retângulo

Teorema de Pitágoras

Em um triângulo retângulo, Figura abaixo, os lados que formam o ângulo reto são denominados catetos e o lado oposto ao ângulo reto é chamado hipotenusa. Os comprimentos da hipotenusa e dos catetos estão relacionados pelo Teorema de Pitágoras

Razões trigonométricas no triângulo retângulo

Para cada ângulo agudo de um triângulo retângulo define-se 6 razões trigonométricas conhecidas como seno, cosseno, tangente, cotangente, secante e cossecante da seguinte maneira

Razões trigonométricas de alguns ângulos notáveis

Exercícios:

1) [Mack-SP] A medida de um ângulo é 225o. Determine sua medida em radianos.

Problema 1.2 [Fuvest-SP] Qual o valor do ângulo agudo formado pelos ponteiros de um relógio à 1 hora e 12 minutos.

2) [UF-PA] Quantos radianos percorre o ponteiro dos minutos de um relógio em 50 minutos?

3) A altura de um triângulo equilátero mede 2 cm. Determine seu perímetro e sua área.

4) A diagonal de um quadrado mede

. Determine seu perímetro e sua área.

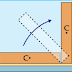
5) No triângulo dado determine as medidas x e y.

6) No triângulo dado sabe-se que c = 5, y = 3 e lado de comprimento a é perpendicular ao lado de comprimento c. Determine a e x.

7) Um carro deve subir uma ladeira de 4 m de altura e percorrer um trecho de aproximadamente

. O inclinômetro do veículo está quebrado e o motorista gostaria de saber qual é o grau de inclinação dessa ladeira. Calcule esse ângulo.

8) Complete as sentenças de modo a torná-las verdadeiras.

9) Preencha os espaços em branco com a medida dos arcos orientados, em graus, que têm origem em A e extremidade indicada em cada quadrante, no sentido anti-horário.